Cloud native EDA tools & pre-optimized hardware platforms
Mie Scattering from a 3D Dielectric Sphere
Tool Used: FullWAVE, MOST
Mie’s solution to Maxwell’s equations, one of the primary formulations for modeling light-particle interactions, describes the scattering of an electromagnetic planewave off a homogeneous sphere. More broadly, the phrase Mie scattering is commonly used to refer to situations where the size of the scattering sphere is comparable to the wavelength of the light, rather than having a much smaller size (Rayleigh scattering) or a much larger size (optical scattering). For Rayleigh and optical scattering, simple and excellent approximations to Mie theory exist that are sufficient to describe the physical behavior. However, for Mie scattering, no simple approximation exists and the full analytic solution, which takes the form of an infinite series of spherical multipole partial waves, is required. Mie scattering arises in a wide variety of applications including atmospheric science, cancer detection and treatment, metamaterials, and parasitology.
FullWAVE, RSoft’s FDTD-based Maxwell equation solver, can be used to directly simulate Mie scattering and produces results in excellent comparison with Mie theory. In this application note, we simulate the Mie problem for a 3D dielectric sphere.
Dielectric Sphere
To simulate the Mie problem, we utilize the enclosed launch excitation type in order to measure the fields scattered by the sphere. For the enclosed launch, a planewave is launched within an enclosed boundary that surrounds the sphere. Outside the enclosed launch boundary, only fields that have been scattered by the sphere propagate; any unscattered light is absorbed at the boundary. Within the enclosed launch boundary, both scattered and unscattered fields are present. The sphere and enclosed launch boundary are depicted in Figure 1.

Figure 1: 3D dielectric sphere (red)
within the enclosed launch region (gold)
For this application note, we will simulate the Mie scattering from a dielectric sphere with the parameters shown in Table 1. In Figure 2, we display the refractive index profile of the sphere, as well as a contour plot of the steady-state electric field amplitude.
| Sphere Diameter | 8.0um |
| Refractive Index of sphere | 1.2 (real) 0.0 (imaginary) |
| Refractive Index of background medium | 1 (air) |
| Free Space Wavelength | 0.75um |
Table 1: Dielectric sphere and simulation parameters

Figure 2: (left) Cross-sectional refractive index profile of the dielectric sphere
(right) Electric field amplitude contour map. The enclosed launch boundary is shown in gold: only fields scattered by the sphere propagate beyond the boundary. The outline of the sphere is shown in black.
To view the far-field scattering pattern, FullWAVE’s MultiPlane Far-Field output options utilize the near-field, as calculated on all sides of the simulation domain, to compute the far-field. Far-field patterns are computed for both the upper (forward scattering) and lower (backward scattering) hemispheres, as shown below in Figure 3.
To view the far-field scattering pattern, FullWAVE’s MultiPlane Far-Field output options utilize the near-field, as calculated on all sides of the simulation domain, to compute the far-field. Far-field patterns are computed for both the upper (forward scattering) and lower (backward scattering) hemispheres, as shown below in Figure 3.

Figure 3: (left) Far-field scattering patterns for the upper and lower hemispheres.
(right) Comparison of far-field scattering patterns with Mie theory. A cut of the far-field scattering patterns is taken along the X-axis [3].
The MIE theory results presented in Figure 3 were obtained using Scott Prahl’s MIE code [4], which is in turn validated against the Wiscombe Mie scattering code [3].
Several physical implications of Mie theory are surprisingly counter-intuitive, as can be seen by plotting the scattering efficiency of the sphere (Qeff=σtot/πa2) vs. its size parameter (x = 2πa/λ0) in Figure 4. Here, λ0 is the vacuum wavelength, a the sphere radius, and σtot the sphere's total scattering cross section (recall that σtot is ∝ to the probability of scattering in any direction [6]).
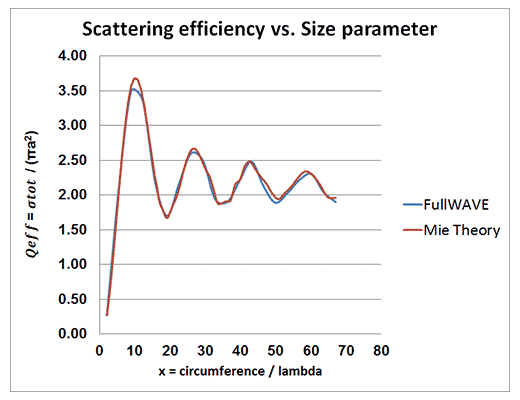
Figure 4: Scattering efficiency (Qeff) vs Size Parameter (x) for the dielectric sphere in Table 1.
Firstly, note that the scattering efficiency approaches 2 in the large particle limit. For large values of the scattering parameter, it might be expected from geometric optics that Qeff = σtot/πa2→ 1 as x → ∞ (as σtot →πa2 in the classical scattering limit). An additional contribution to σtot, however, arises from the diffraction of the incident plane wave at the edges of the sphere. For a dielectric sphere, the additional contribution to σtot is ≈πa2, and thus σtot → ≈2πa2 and Qeff→ ≈ 2 as x→∞. This effect is referred to as the "extinction paradox", and is discussed in detail in [2]. Note that the reason for the approximate figures above is due to field penetration into the dielectric sphere. For a perfectly conducting sphere, where the field does not penetrate into the sphere, σtot → πa2 and Qeff→ 2.
Secondly, note that Mie theory predicts that the scattering efficiency oscillates with the size parameter at intermediate particle sizes. In the Rayleigh regime(0<x<0.1), the scattering efficiency can be written as
is the ratio of the refractive index of the particle to that of the surrounding medium. Therefore, in the Rayleigh regime, the scattering efficiency is simply proportional to x4. In the optical scattering regime, Qeff→ ≈ 2. However, in the intermediate regime, the scattering efficiency is seen to oscillate as the size parameter increases.
MOST, RSoft's scanning and optimization utility, was used to automate multiple FullWAVE simulations to produce the Qeff vs. x plot in Figure 4. The quantity σtot is easily computed in FullWAVE using the MultiPlane Far-Field output options; after obtaining σtot, Qeff and x are then generated for Figure 4 using post processing. The MIE theory results presented in Figure 4 were obtained using Phillip Laven's MIE code [5], which is in turn validated against the Bohren and Huffmann MIE code [2].
In summary, FullWAVE provides a powerful and accurate method for simulating the Mie problem. The results presented in this application note for scattering from a simple dielectric sphere can be easily extended to more complicated situations, giving users a versatile tool to study a wide variety of applications in atmospheric science, biophotonics, advanced materials, and more.
Learn More
- Download simulation file (zipped file, 2KB) from SolvNetPlus (account required, please log in first)
References
[1] Tseng, Snow H., et al. "Pseudospectral time domain simulations of multiple light scattering in three‐dimensional macroscopic random media." Radio science 41.4 (2006).
[2] Bohren, Craig F., and Donald R. Huffman. Absorption and scattering of light by small particles. John Wiley & Sons, 2008.
[3] W. J. Wiscombe, "Improved Mie scattering algorithms," Appl. Opt. 19, 1505-1509 (1980)
[4] http://omlc.org/calc/mie_calc.html
[5] http://www.philiplaven.com/mieplot.htm
[6] Cox, A. J., Alan J. DeWeerd, and Jennifer Linden. "An experiment to measure Mie and Rayleigh total scattering cross sections." American Journal of Physics 70.6 (2002): 620-625.





