Cloud native EDA tools & pre-optimized hardware platforms
Computing Bending Modes
The calculation of bending waveguide modes is essential to the design of Planar Lightwave Circuits (PLCs) and other waveguide-based photonic devices. Bending waveguides introduce shifts in the mode shape and bending losses which, as a function of the waveguide radius, determine the minimum bending radius as well as the minimum size of the PLC. We will use a simulated bend in FemSIM to calculate the bending mode.
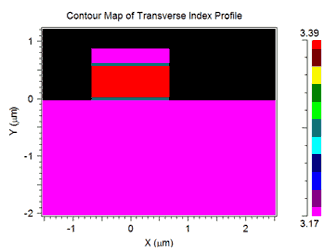
As an example, we will compute the fundamental bending mode of a simple ridge waveguide shown here. It has a width of 1.4 μm and consists of an InGaAsP guiding layer (n= 3.39) and an InP cap layer and substrate (n = 3.17). The operating wavelength is 1.55 μm.
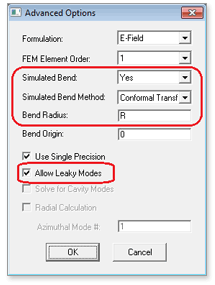
To enable the calculation of a bending mode, we need to make several settings in the FemSIM Advanced Options dialog box:
- Simulated Bend: Yes
- Simulated Bend Method: Direct. This enables the use of a cylindrical form of Maxwell’s equations to directly solve for bending modes.
- Bend Radius: R. This is a symbol we defined to represent the bending radius and has a value of 50 μm.
- Allow Leaky Modes: selected, since bending modes are inherently leaky.
We also set a PML Width of 0.5 μm in the FemSIM Simulation Parameters dialog.
The calculated TE (top) and TM (bottom) fundamental bending modes are shown below. The Ex (left), Ey (center), and a vector plot of the transverse E field (right) are shown.

These leaky modes profiles are clearly shifted from the center of the guiding layer and the vector plot shows that the polarization has been slightly rotated. The TE bending mode has a modal effective index of 3.262488 + i2.702e-06. The imaginary part of the effective index (ni) is related to the loss as 54.5474*ni/lambda. For this mode, the loss is 0.95 dB/cm.
We can also study the loss vs radius using the MOST scanning tool. The results for the fundamental TE and TM modes are shown here:
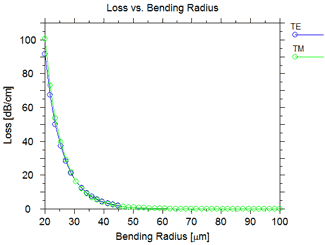
Understanding the mode profiles and loss of bending modes is critical for designing PLCs. These types of modes can easily be computed using the simulated bend feature.





