Cloud native EDA tools & pre-optimized hardware platforms
The Abbe sine condition, named after Ernst Abbe, is a fundamental principle in optics that describes the conditions for an undistorted pupil mapping between object space and image space. Originally formulated to facilitate the design of microscopes, it later came to be used throughout optical design to correct field-linear aberrations (i.e., coma) without tracing a large number of rays. While these ray trace savings are less important in the modern context, the Abbe Sine Condition remains a powerful tool for understanding performance over the field at a glance.
Ernst Abbe: A Pioneer in Optics and Social Reform
Before discussing the insights of Abbe’s sine condition, the authors would first like to share a few aspects of Abbe’s life. Born in 1840 in Eisenach, Germany, Abbe's career in optics coincided with the nascent stages of the modern optics industry. At a time when the industrial revolution was transforming society, Abbe believed that industry should care not only about the work it produced but also about the workers. To this end, he advocated for a range of pioneering social reforms, including the 8-hour workday, paid vacations, retirement benefits and severance pay, and equality measures in hiring. Many of his ideas were revolutionary at the time [1]. Readers interested in this aspect of Abbe’s life are encouraged to read "Ernst Abbe and his work," by H. Volkmann.

Universitätsbibliothek Heidelberg, CC BY-SA 4.0, via Wikimedia Commons
A Visionary in Optics
Ernst Abbe's contributions to the field of optics are equally commendable. His name is synonymous with several key concepts and equations that continue to influence optical science to this day. Some of his remarkable contributions include:
- Abbe diagram
- Abbe number
- Diffraction Limit Equation (Helmholtz also had a derivation)
- Abbe error
- Abbe prism
- Abbe refractometer
- Abbe condenser
- Numerical Aperture
- Abbe Sine Condition
The Abbe diagram, named in his honor, is a fundamental tool for understanding the properties of optical glasses in terms of their refractive index and Abbe number. He was instrumental in developing the concept of numerical aperture, a crucial parameter in optical systems. Abbe's work laid the foundation for improved microscope performance. Even at this day, many of his works remain a captivating read, showcasing his ability to convey complex ideas in a highly accessible manner.
Fundamentals of the Abbe Sine Condition
Mathematically, the Abbe Sine Condition [2] is the requirement that the ratios of the numerical apertures of the ray angles is constant between object space and image space for all zones of the pupil; this constant is equal to the magnification. The magnification can be considered for both finite conjugate and infinite conjugate when there is no spherical aberration present.

Figure 1. Visualization of the ray bundles for a system of unit magnification satisfying the Abbe Sine Condition when no spherical aberration is present. Note that U and U* are the ray angles for an arbitrary zone of the pupil in object and image space, respectively. The ray angles in Abbe sine condition are not limited to the edge rays at full aperture.
If the Abbe Sine Condition is not met, the magnification of a finite conjugate system will be different for different zones of the pupil. If the object is at infinity, the focal length of the system will be different for different zones of the pupil. Either condition leads to the fact that different zones of the pupil will create images of different sizes. With some thought, it can be recognized that this condition is equivalent to the presence of coma.
If the Abbe Sine Condition is met, then the magnification (or focal length, for an infinite conjugate system) will be constant across the pupil, including in the paraxial region. In other words, the magnification (or focal length) will converge to the paraxial value. This leads to the traditional expression for the Abbe Sine Condition:
where u, u* are the paraxial ray angles.
By observing that the sines of angles are proportional to numerical aperture, we can see that, at its heart, the Abbe Sine Condition is about ray bundles of equivalent NA mapping to each other. As such, the Abbe Sine Condition is a property of the energy of the system and is not just a property of conventional ray optics [3]. The benefit of understanding the Abbe Sine Condition is that it allows coma in an optical system to be estimated by looking at the difference in angles, and subsequently found with minimal effort.
Implications of the Abbe Sine Condition
One implication of the Abbe Sine Condition is that the principal “planes” for a system satisfying it become spherical rather than planar if the optical system is both well-corrected and extends beyond the paraxial regime. (Note: When generalized beyond the paraxial regime, the concept of principal planes becomes the locus of points of equivalent refraction.) For simplicity, the two idealized systems with objects at infinity are depicted in Figure 2. In Figure 2a, each ray is propagated forward from object space and mapped to a spherical rear principal “plane.” This mapping shows that the equivalent output angle in image space is based on the sine of the ray height and rear focus. More specifically, Figure 2a maps incremental changes in ray heights to incremental changes in the sines of the ray angles, so the system satisfies the Abbe Sine Condition. In Figure 2b, each ray is also mapped from object space and mapped to a planar rear principal “plane.” In this instance, to achieve an equivalent ray height from object space to image space, we must use the tangent of the angles, rather than the sines. Again more specifically, Figure 2b maps incremental changes in ray heights to incremental changes in tangents of the ray angles. Such a system would violate the Abbe Sine Condition.
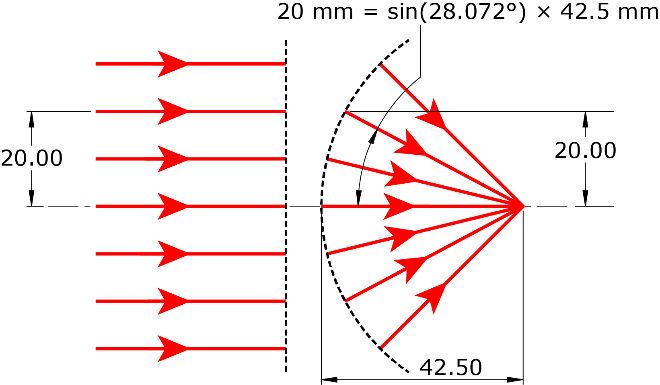
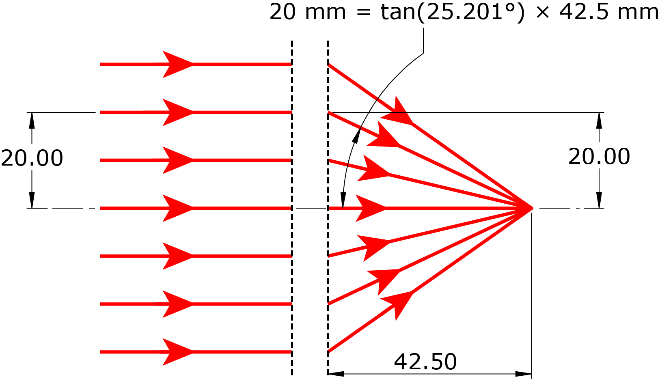
Figure 2. Equidistant object-space rays mapped onto a rear principal “plane” that is (a) spherical vs (b) flat. Case (a) satisfies the Abbe Sine Condition; case (b) does not.
Of course, in the paraxial regime for which principal planes are intended, sine, tangent, and radial angle are all approximately equal, and the principal planes are approximately flat. Nevertheless, this distinction has practical implications.
Abbe Sine Condition and Parabolic Mirror
Let us begin by examining the optical properties of a single parabolic mirror in the context of the Abbe Sine Condition. As readers may know, a parabolic mirror forms a stigmatic image on-axis of an object at infinity (that is, there is no spherical aberration) but quickly becomes limited by coma as image height increases (see Figure 3).

(a)

(b)

(c)
Figure 3. (a) Parabolic reflector with (b) zero aberrations on-axis and (c) off-axis wave fan contains coma.
To visualize this behavior in the context of the Abbe Sine Condition, we first observe that the locus of equivalent refraction (being the parabolic mirror itself) is necessarily not spherical. Consequently, if we attempt to replicate Figure 2a by drawing a pair of rays that satisfy the Abbe Sine Condition, those rays would necessarily be non-physical. These non-physical rays, which experience a discontinuity caused by the mismatch between the parabolic mirror and the spherical locus of equivalent refraction, are depicted in Figure 4.

(a)

(b)
Figure 4. Parabolic reflector showing the intended ray heights (a) and what the projected ray heights are for the parabola. The discontinuities for this height difference (b) are also highlighted.
Abbe Sine Condition and a Single Flat Optic
Let us now consider a system whose only powered element is a single flat optic (e.g., a metalens, diffractive, or Fresnel lens). For such a system, the front and rear principal planes are coincident on a single optical surface and are necessarily flat. Thus, the locus of equivalent refraction for this system is planar (as in Figure 2b) and therefore cannot simultaneously satisfy the Abbe Sine Condition and achieve perfect imaging performance. Consequently, designers would have to balance the field-linear aberrations (i.e. coma) introduced by the surface using typical coma correction means, such as via the introduction of spherical aberration and stop-shifting [5].
To visualize this example, we can take this single flat optic and project the rays necessary to satisfy the Abbe Sine Condition, shown in Figure 5. These ray paths are clearly non-physical: there is a large discontinuity between the ray heights in object space and image space. The image-space angles are being driven by sines and the image-space heights, not being driven by tangents.

Figure 5. Example flat optical surface where rays are mapped from infinite conjugate object space to a focus in image space that would be necessary to satisfy the Abbe Sine Condition.
Abbe Sine Condition and Plano-Convex Lenses

Figure 6. How to orient a plano-convex singlet? Both lenses are corrected for spherical aberration by optimizing the conic on the curved surface. Abbe Sine Condition tells us that the conic on the front surface will have less coma.
We conclude by generalizing a question often posed to optics students in the context of spherical aberration: which way should you orient a plano-convex lens? If the powered surface is merely a sphere and the goal is to improve on-axis performance, then (as optics students learn) the front-side-curved approach depicted on the left in Figure 6 is correct.
But what if the spherical aberration is corrected (for instance by making the powered surface aspheric), and the goal to improve performance over the field: Is the front-side-curved orientation still preferred? The answer is it is still preferred because that orientation is closer to satisfying the Abbe Sine Condition and thereby minimizes coma. For the rear-side-curved lens, the rear locus of equivalent refraction is a sphere of the opposite sign than what the Abbe Sine Condition would desire, resulting in significantly more coma.
Conclusion
The Abbe Sine Condition serves as a fundamental guiding principle in the world of optics, shedding light on basic principles of optical system design. From parabolic mirrors to single flat-powered optics and plano-convex lenses, the Abbe Sine Condition plays a pivotal role in our understanding of optical aberrations. If a single optical surface/element violates the Abbe Sine Condition, the coma it generates can be corrected elsewhere in the system, so that the full system still obeys the Abbe Sine Condition. The Abbe Sine Condition is a fundamental principle that is applicable to all optical systems, even those that use unconventional optics. It is not limited to ray optics. By recognizing the limitations and requirements of the Abbe Sine Condition, optical designers can make informed choices and optimize optical systems for superior performance and minimal aberrations.
References
[1] Volkmann, H., "Ernst Abbe and his work." Applied optics 5.11 (1966): 1720-1731.
[2] Abbe, E., “Beitrage zur Theorie des Mikroskops und der mikroskopischen Wahrnehmung,” Arch. fuer mikroskopische Anat. 9, 413–468 (1873).
[3] Mansuripur, M., "Abbe's Sine Condition," Opt. Photon. News 9(2), 56-60 (1998).
[4] Braat, J. J. M., “The Abbe sine condition and related imaging conditions in geometrical optics,” Proc. SPIE 3190, 59–64 (1997).





