Cloud native EDA tools & pre-optimized hardware platforms
Photonic Solutions Enewsletter
February 2016
Creating a Pulse Train in FullWAVE Using Custom Time Envelopes
Mode-locked lasers, which generate a train of ultra-short pulses, have become an important tool in precision optical frequency measurement [1] and are useful for the design of future ultrahigh-speed optical communication systems [2]. This note will discuss how to use FullWAVE™'s custom time envelope feature to create this type of pulse train. Details about generating a custom time envelope can be found in Section 4.B.2 of the FullWAVE manual. Users can access design files on the Customer Support Portal.
The output of a mode-locked laser is a comb of equidistant lines in the frequency domain, separated by a bandwidth of frep. In the time domain, this corresponds to a train of pulses whose temporal separation is given by the cavity round-trip time trt = 1/frep. The offset of the comb, fceo is connected to the pulse-to-pulse phase slip
Δϕ = 2π(fceo/frep). We are going to create a pulse train with fceo = frep/4 , such that every fifth pulse is identical, as shown in Figure 1 [3].

Figure 1. Pulse Train with fceo = frep/4, such that every fifth pulse is identical
The electric field of such a pulse train can be written as:
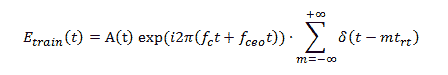
(1)
where A(t) denotes the pulse envelope and fc = c/λ is the central frequency of the comb and the function δ(t – mrrt) function produces the pulse train. Note that the time envelope equation for FullWAVE’s Pulse excitation type, as described in Section 4.D.2 of the FullWAVE manual, is:

(2)
The custom envelope in Eq.(1) can be written as

(3)
And the excitation wavelength will be modified by fceo term and become
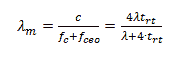
(4)
Using the above analysis, a simple model has been created in the design file pulsetrain.ind. We created the following symbols to help with the definition:
|
Note that we have also enabled the Excitation Time Waveform option in the Output Options dialog so that we can view the time envelope used in the simulation. The animated results of the FullWAVE simulation are shown in Figure 2 and the excitation envelope is shown in Figure 3. Red lines indicate the pulse center and the green curve shows the envelope of each pulse.
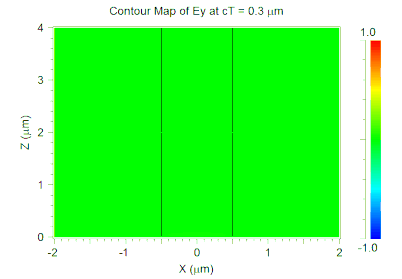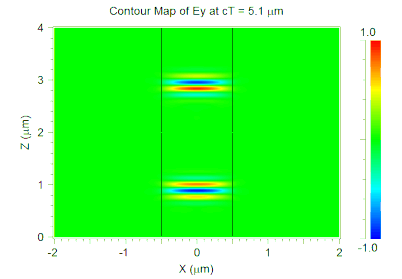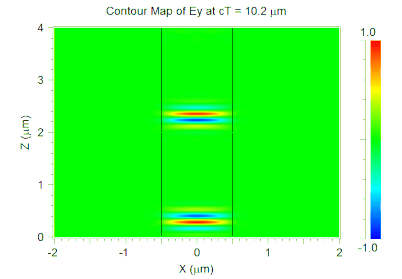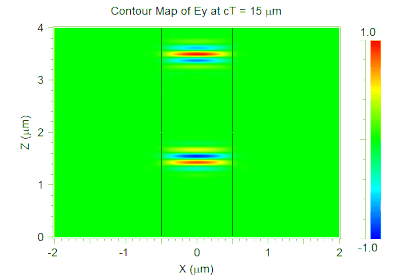
Figure 2. Pulse train propagating in a waveguide

Figure 3. The pulse train recorded as time waveform (.pstm file).
The red lines have been added as WinPLOT drawing options in this plot.
Please contact our technical support team at rsoft_support@synopsys.com for more information.
References
- David J. Jones,Scott A. Diddams et al. “Carrier-Envelope Phase Control of Femtosecond Mode-Locked Lasers and Direct Optical Frequency Synthesis,” SCIENCE VOL 288 28 APRIL 2000.
- M. Jacquey, S. Bonhommeau, and M. A. Bouchene, “Experimental demonstration of phase control of dispersion effects for an ultrashort pulse train propagating in a resonant medium,” OPTICS LETTERS / Vol. 28, No. 14 / July 15, 2003.
- Fabian Lücking, Dissertation “Carrier-Envelope Phase Control for the Advancement of Attosecond Pulse Generation,” 2014.






